Análise Combinatória: Dicas para lidar com ela no vestibular
A Análise Combinatória é, de fato, um assunto muito interessante da matemática. Além de ser muitíssimo útil para determinadas atividades profissionais, ele aparece com uma boa frequência nos vestibulares em geral. Basicamente, a Análise Combinatória tem como finalidade calcular o número de maneiras de combinarmos elementos de um ou mais conjuntos para obtermos determinados agrupamentos. No estudo da Análise Combinatória, dois tipos de agrupamentos são de grande importância:
- agrupamentos que diferem entre si pela ordem dos elementos do grupo e/ou pelos elementos componentes (sequências);
- agrupamentos que diferem entre si somente pelos elementos componentes (conjuntos).
Vamos exemplificar os dois tipos. Por exemplo, considere os algarismos 1, 2 e 3.
- Podemos formar 6 sequências de 2 elementos distintos.
(1,2), (2,1), (1,3), (3,1), (2,3) e (3,2)
Observe que a sequência (1,2) é diferente da sequência (2,1).
Portanto, nos problemas em que a ordem dos elementos no agrupamento é importante, trata-se de sequências.
- Podemos formar 3 conjuntos de 2 elementos:
{1,2}, {1,3} e {2,3}
Observe que aqui não vale pegar o conjunto {2,1}, pois esse conjunto é o mesmo que {1,2}.
Portanto, nos problemas em que a ordem dos elementos não altera o agrupamento, trata-se de conjuntos.
O número de sequências pode ser obtido pelo Princípio multiplicativo (Princípio fundamental da contagem) enquanto o número de conjuntos pode ser obtido por:
Vamos mostrar uma aplicação de cada tipo:
- Uma moça dispõe de 5 blusas, 4 saias e 3 casacos. De quantos modos ela pode se vestir, se cada traje deve ser formado por uma blusa, uma saia e uma casaco?
Resolução:
Há 5 possibilidades para escolher uma blusa, 4 possibilidades para escolher uma saia e 3 possibilidades para escolher um casaco.
Pelo Princípio multiplicativo, o número de trajes é dado por:
5 x 4 x 3 = 60
Assim, essa moça poderá se vestir de 60 modos diferentes, ou seja, de 60 modos sem repetir o mesmo traje.
- Numa sala com 20 alunos, de quantos modos podemos escolher 3 alunos para representá-la em um evento?
Resolução:
Nesse caso, devemos utilizar a fórmula de Combinações simples. Como temos 20 alunos, o número de possibilidades para a escolha de 3 deles é:
Assim, podemos escolher diferentes trios de alunos de 1140 modos, sendo que dois trios quaisquer terão sempre, pelo menos, um aluno diferente.
Observação:
Do exposto, pode-se concluir que:
- Determinados problemas clássicos podem ser resolvidos pelo Princípio multiplicativo. São exemplos: quantidade de números que tenham um determinado número de algarismos; senhas de banco; placas de automóveis; números de telefones; códigos em geral; disposição de pessoas em lugares de um veículo; combinação de roupas para formar trajes diferentes; número de trajetórias para se ir de um lugar a outro.
- Determinados problemas clássicos podem ser resolvidos pela fórmula das combinações simples ( ). Alguns exemplos são: formação de comissões de pessoas; número de retas; número de triângulos; número de diagonais de um polígono; número de subconjuntos de um conjunto dado; combinação de substâncias químicas para formar uma mistura, formação de times esportivos.
Uma nota:
Nas permutações simples, utilizamos o princípio multiplicativo, por exemplo, na obtenção do número de anagramas de N letras formadas com as N letras de uma determinada palavra; na disposição de N pessoas em N lugares determinados; na disposição de N pessoas para formar uma fila.



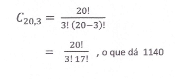




ID: {{comments.info.id}}
URL: {{comments.info.url}}
Ocorreu um erro ao carregar os comentários.
Por favor, tente novamente mais tarde.
{{comments.total}} Comentário
{{comments.total}} Comentários
Seja o primeiro a comentar
Essa discussão está encerrada
Não é possivel enviar novos comentários.
Essa área é exclusiva para você, assinante, ler e comentar.
Só assinantes do UOL podem comentar
Ainda não é assinante? Assine já.
Se você já é assinante do UOL, faça seu login.
O autor da mensagem, e não o UOL, é o responsável pelo comentário. Reserve um tempo para ler as Regras de Uso para comentários.