Conheça as 5 equações que revolucionaram a Matemática e a Física
Quando falamos de uma equação geralmente pensamos no trabalho que será tentar resolvê-la. Afinal, qual o sentido de procurarmos o valor de x? Muitas vezes esquecemos que uma simples equação pode guardar ideias que transformaram nossas vidas de modo definitivo, proporcionando um desenvolvimento tecnológico que seria impossível sem as suas soluções.
O mundo das equações, propriamente dito, é muito mais amplo do que imaginamos. Existem as equações cujas soluções são números, as que têm matrizes como soluções e até mesmo equações funcionais, nas quais suas respostas, como o nome sugere, são funções.
Assim, o desafio de escolher as 5 equações que mudaram o mundo ganha uma dimensão enorme, pois qual seria o critério mais adequado?
Para tentar encontrar uma solução para esse "problema", é preciso analisar as equações que:
- por alguma razão ficaram mais famosas e causaram maior impacto em atrair novos talentos para estudos sobre Ciências ou Matemática
- geraram maior mudança no dia-a-dia das pessoas
- causaram maior mudança no meio científico, permitindo novas descobertas
- são as mais "belas", pois de modo conciso representam belas ideias ou imagens
Com base nisso, segue as 5 equações mais importantes do mundo, com base na minha opinião pessoal:
- Teorema de Pitágoras
A primeira equação é provavelmente a mais conhecida.
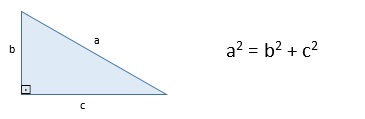
Em um triângulo retângulo o quadrado da medida da hipotenusa é igual a soma dos quadrados das medidas dos catetos é igual.
Acredita-se que esta relação foi descoberta e demonstrada pelo pensador grego Pitágoras (570 a.C. – 495 a.C.), entretanto, há quem diga que ela já existe muito antes.
Ela vem para a lista por ser talvez a relação matemática mais utilizada no dia-a-dia, pois sempre que precisamos determinar comprimentos, ela possivelmente está presente. Ou seja, todas as construções que existem no mundo, vemos o teorema de Pitágoras.
Outra grande mudança provocada por esse teorema, foi que a partir dele é atribuída a descoberta dos números irracionais: aqueles que não podem ser representados como uma razão entre dois números inteiros. Isto foi uma enorme transformação na época, pois acreditava-se em um universo racional, isto é, tudo poderia ser representado por razões entre números inteiros.
- Segunda Lei de Newton
A segunda equação dessa lista foi escolhida porque com ela veio o desenvolvimento de toda uma área da Matemática: o cálculo diferencial, ferramenta fundamental para todas as outras equações que vem pela frente e que nos permitiu grandes avanços nas mais diversas áreas.
A mudança de movimento é proporcional à força motora imprimida, e é produzida na direção de linha reta na qual aquela força é aplicada.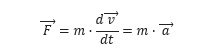
Esta relação enunciada por Isaac Newton (1643 d.C. – 1727 d.C.), mudou como vemos não apenas como entendemos os movimentos, mas de modo indireto como vemos toda a Matemática.
- Teorema fundamental do Cálculo
A terceira relação, apesar de não ser familiar para um estudante do ensino médio, permite a ligação entre os conceitos de taxa de variação de uma função, que nos fornece as tendências de crescimento ou decrescimento (cálculo diferencial) e o cálculo acúmulos (cálculo integral). De modo conciso e elegante, essa equação facilitou o desenvolvimento de muitas das teorias que estudamos atualmente e nas mais variadas áreas do conhecimento como Engenharia, Economia, entre outras.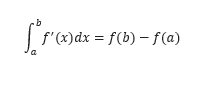
- Equações de Maxwell
A próxima escolha na realidade é um conjunto de quatro equações formulados por James C. Maxwell (1831 d.C. – 1879 d.C.). Com elas ele unificou todos os fenômenos elétricos e magnéticos estabelecendo conexões entre diversas teorias, criando uma das mais belas e teorias já feitas.
Utilizando cálculo vetorial, elas são
- Teoria de relatividade de Einstein
Fechamos nossa lista com uma equação que representa uma mudança em como vemos a Física. Nela Albert Einstein (1879 d.C. – 1955 d.C.) relacionou massa e energia e afirmou que a massa transforma em energia.
Em que E é a energia, m a massa e c uma constante que representa a velocidade da luz no vácuo.
Apesar de um pouco distante do nosso dia-a-dia, ela trouxe a Física para a cultura pop, contribuindo para difundir ideias e despertar o interesse de toda uma nova geração para o estudo das Ciências Exatas. Por esse motivo, ela merece a quinta cadeira em nossa seleção.
O que torna essas equações tão importantes é que sem elas você possivelmente não estaria neste momento lendo este texto em seu computador ou smartphone, nem com as luzes acesas em sua casa, pois foi com elas que tudo isso se tornou realidade.
Espero que esta breve seleção desperte agora o interesse em saber mais sobre essas e outras equações que, infelizmente, ficaram de fora desta lista. Que sirva como um convite para conhecer mais sobre a apaixonante história das Ciências Exatas!
Bom estudo!

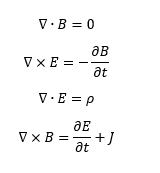
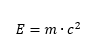

ID: {{comments.info.id}}
URL: {{comments.info.url}}
Ocorreu um erro ao carregar os comentários.
Por favor, tente novamente mais tarde.
{{comments.total}} Comentário
{{comments.total}} Comentários
Seja o primeiro a comentar
Essa discussão está encerrada
Não é possivel enviar novos comentários.
Essa área é exclusiva para você, assinante, ler e comentar.
Só assinantes do UOL podem comentar
Ainda não é assinante? Assine já.
Se você já é assinante do UOL, faça seu login.
O autor da mensagem, e não o UOL, é o responsável pelo comentário. Reserve um tempo para ler as Regras de Uso para comentários.