A curva exponencial e o coronavírus

*Por Rodney Brasil Luzio, professor de matemática do Anglo Vestibulares

Nas últimas semanas, não houve assunto mais comentado no mundo do que a pandemia do novo coronavírus, batizado de Covid-19. Os primeiros casos ocorreram na cidade de Wuhan, na China, em meados de dezembro do ano passado, e o vírus tem se alastrado rapidamente pelo mundo todo. As informações sobre o crescimento dessa pandemia jogam luz para um conceito importante da Matemática: o crescimento exponencial.

A Matemática, entre outras funções, nos ajuda a entender fenômenos e situações do nosso cotidiano. É muito comum que as informações trazidas pelos meios de comunicação sejam amparadas por números que dimensionam e qualificam a notícia. Situações de crescimento e decrescimento são mais comuns quando estão ligadas ao conceito de linearidade, ou seja, a uma lógica que demonstra a taxa de aumento ou de declínio constante. No entanto, os números mostram que, no caso dessa pandemia, o crescimento não é linear, mas exponencial.

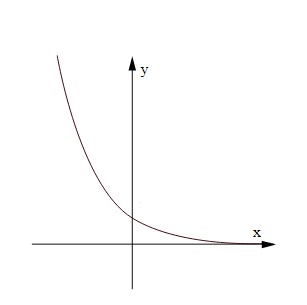
O estudo das funções tem como objetivo modelar situações que nos ajudam a compreender o fenômeno analisado e poder agir sobre ele. A exponencial é uma função escrita na forma f(x) = a^x , com  1 ≠ a > 0, sendo a um número real,  que descreve situações de crescimento e decrescimento que podem começar de maneira lenta, mas que se acentuam de forma extremamente rápida. Graficamente, esse comportamento pode ser expresso pelos gráficos abaixo:

Exponencial crescente

Exponencial decrescente

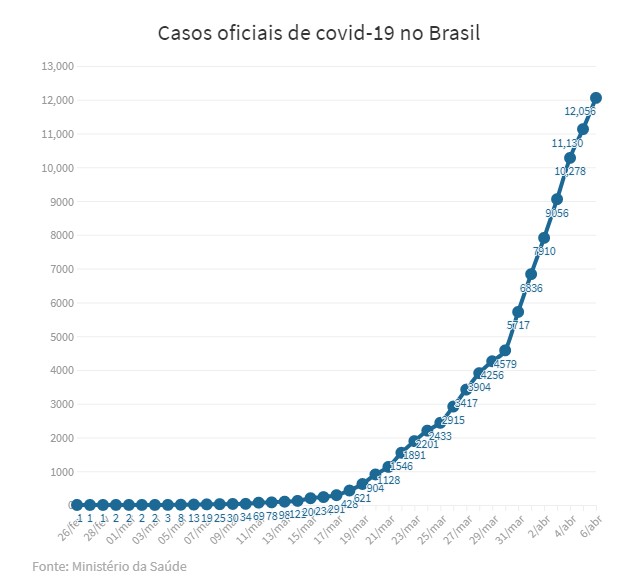
Comparando as curvas acima com o gráfico abaixo, podemos notar o crescimento exponencial nos casos oficiais da Covid-19 no Brasil entre 26/02/2020 e 06/04/2020:

O comportamento exponencial pode ser observado em diversas áreas do conhecimento, como na Biologia – número de micro-organismos em uma cultura; na Economia – juros compostos; na Física – quebra de átomos em uma fissão nuclear; na Química – conceito de meia vida dos átomos radioativos; entre outros. No caso dessa pandemia, o que se espera é que haja um pico nesse crescimento, estabilidade e, mais uma vez, uma curva com rápido declínio, ou seja, a curva passe de exponencial crescente para exponencial decrescente.

Nos exames vestibulares, o conceito de exponencial aparece tanto em questões relacionadas às modelagens em funções, quanto em exercícios de progressão geométrica ou em juros compostos, como já mencionado. Na maioria deles, o que se cobra do aluno é a habilidade em perceber o padrão estabelecido pela situação descrita. É muito importante saber diferenciar e não confundir os conceitos desse conteúdo com os de função afim ou de função quadrática, que apresentam comportamentos diferentes em relação à exponencial.

Dessa maneira, analisar comportamentos expressos em gráficos é de fundamental importância na preparação para os exames vestibulares e o Enem. A leitura de um gráfico, a partir da relação estabelecida pelas grandezas envolvidas e, com as propriedades do modelo descrito, é condição essencial para se poder tirar conclusões acertadas sobre o fenômeno descrito e, assim, entender cada vez mais a realidade que nos cerca.