O infinito de Pi: como o 3,14 revolucionou e facilitou a Matemática

*Por Glenn van Amson

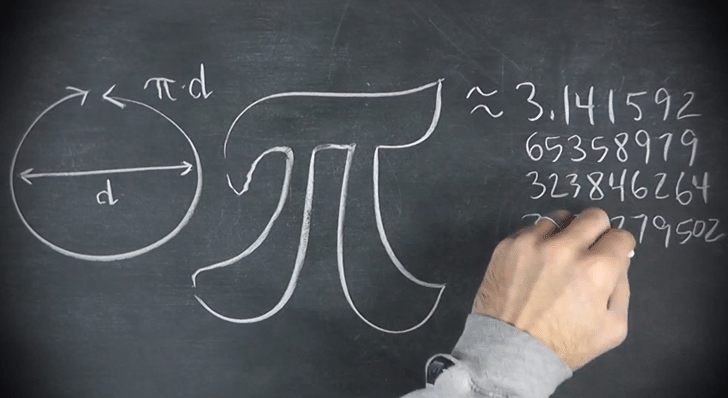
Uma vez o sr. Chico, então chefe da manutenção da empresa em que eu trabalho, me pediu ajuda para calcular o comprimento de um murinho a ser levantado rente a um canteiro circular. Quando ele me contou que o tamanho do canteiro era de 2 metros, fiz uma pergunta e concluí que ele se referia ao diâmetro. Eu disse então que o muro deveria ter uns 6,3 metros de comprimento. Ele agradeceu, mas quis saber qual o cálculo a ser feito nesses casos. Eu respondi que bastava multiplicar o diâmetro por 3,14 e ele se deu por satisfeito.

Na verdade, todo estudante do Ensino Médio usa a fórmula C = 2 ⋅ p ⋅ r, para calcular o comprimento C da circunferência de um círculo de raio r. A letra grega p (leia-se pi) representa uma constante cujo valor aproximado é 3,14. Acho que o sr. Chico usa, até hoje, a fórmula C = p ⋅ d, em que d é a medida do diâmetro. As duas fórmulas são equivalentes, pois d = 2r.

Muitos processos de cálculos de comprimentos, áreas e volumes já eram conhecidos há séculos; eles vinham na forma de instruções de procedimentos e não como fórmulas como, por exemplo, C = 2pr, A = pr², V = pr³. Essas e outras fórmulas consequentes apareceram apenas a partir do Renascimento. Até aí a constante p não era o foco. Usavam-se valores aproximados como 3,  e 3,14.

O trabalho de Archimedes (século 3^o a.C), para obter valores mais exatos de p, pode ser destacado como sendo um dos primeiros em que a preocupação era com o número p em si. Com o tempo, este número rendeu inúmeros estudos matemáticos. Provou-se que ele é um número irracional; isto é, não existem números inteiros a e b, tais que  = p. A expansão decimal de p não apresenta padrões elementares; é como se suas casas decimais vieram de uma caixa de surpresas. Veja algumas delas.

p = 3,14159265358979323846264338327950288419719399375105820974..

Por outro lado, há igualdades com padrões bonitos, como, por exemplo, em  = 1 –  +  –  +  –  + .. +  + .. , ou em  =  +  +  + .. +  + ..

As teorias elaboradas sobre o p geram muita 'matéria prima' para as mais diversas áreas na Matemática e na Computação. Pode-se criar processos de criptografia para codificar mensagens.

Em 13 de março 2015, o japonês Akira Haraguchi  'recitou', de cabeça, o p com 111700 casas decimais. Para nós que não temos tanta capacidade de memória, existem os versos como recurso. Exemplo:

p = 3,14159265358979323846

Para a imensa maioria das pessoas é muito mais simples: p é um número importante, que vale aproximadamente 3,14 e, para muitas pessoas, 3/14 corresponde ao dia 14 de março e, assim, essa data foi escolhida como o 'Dia do p'.